数模算法总结
数模算法总结
下面这些算法分类并不绝对,有的算法可能同时属于好几类,但是只写在一类里。
算法类型
矩阵分解


奇异值分解
SVD,被用于PCA算法。
主成分分析
PCA数据降维。
属性约简算法
Relief算法
基于邻近实例的思想。
RoughSets算法
粗糙集理论。
关联规则挖掘算法
可以用来找出数据集中频繁出现的数据集合。
比如在一堆的购物清单中,找出 {牛奶、面包} 经常被一起购买。
拓展一下,用于判断单词中哪个词根词缀出现的最多。
Apriori算法
通过对数据逐层迭代的方法,比较耗时。
产生大量的候选项目集,会消耗大量的内存。
AprioriAll算法
改进Apriori算法,通过候选序列的逐级扩展和剪枝策略来减少搜索空间。
GSP算法
与AprioriAll算法相比,GSP算法计算较少的候选集,并且在数据转换中不需要事先计算频繁集。
对于序列模式的长度比较长的情况,算法难以处理。
PCY算法
改进Apriori算法,引进了哈希函数,降低Apriori算法频繁的扫描数据库,降低候选项集所占用的内存。
由于哈希函数的原因,有些非频繁项被映射到了频繁桶中,导致这部分非频繁项很难被过滤掉
多阶段算法
改进PCY算法,解决PCY算法非频繁项被映射到了频繁桶中的问题。
多哈希算法
与PCY算法基本一致,使用多个哈希表。
FP-Tree算法
对数据库进行两次扫描便可以对所有可能的频繁项进行计数(更快)。
FP-Tree算法主要分为两个步骤:构建FP树和频繁模式挖掘。
XFP-Tree算法
改进FP-Tree算法,XFP-Tree算法旨在并行的构建FP树来提升效率(更更快)。
PrefixSpan算法
高效但内存消耗较大。
分类与回归算法
ID3算法
信息增益选择特征。
ID3算法的核心是根据信息增益来选择进行划分的特征,然后递归地构建决策树。
C4.5算法
信息增益率选择特征。
ID3算法的一种延伸和优化。
CART算法
基尼系数选择特征。
能够处理连续型特征和离散型特征。
容易过拟合,需要设置合适的阈值控制树的深度;
对于缺失值的数据,需要进行填充或忽略处理。
分类决策树
对于大规模数据集,构建决策树的时间复杂度较高。
回归树
对于非线性数据或噪声数据,回归树的预测精度可能较低。
K-NN算法
可以用来做分类也可以用来做回归。
计算量大。
贝叶斯算法
朴素贝叶斯分类算法
过滤垃圾邮件。
朴素贝叶斯法是基于贝叶斯定理与特征条件独立性假设的分类方法。
贝叶斯回归
叶斯回归不仅给出了预测值,同时也提供了预测的不确定性(即预测值的分布)。
关联规则分类算法(CBA)
利用了Apriori挖掘出的关联规则,然后做分类判断。
支持向量机(SVM)
支持线性、非线性。
随机森林算法
噪声较大的样本集容易过拟合。
聚类算法
无标签。
k-Means算法
对异常数据敏感
k-means++算法
对k-means中初始质心点选取的优化算法。
bi-kmeans算法
对kmeans算法会陷入局部最优的缺陷进行的改进算法。
模糊C均值聚类算法
软聚类。
期望最大化算法(EM)
一种迭代优化算法,用于估计概率模型的参数。用于隐马尔可夫模型(HMM)、高斯混合模型(GMM)等。
隐马尔可夫模型(HMM)
可以用于无监督学习和监督学习。
高斯混合模型(GMM)
适用于软聚类和复杂的簇形状。
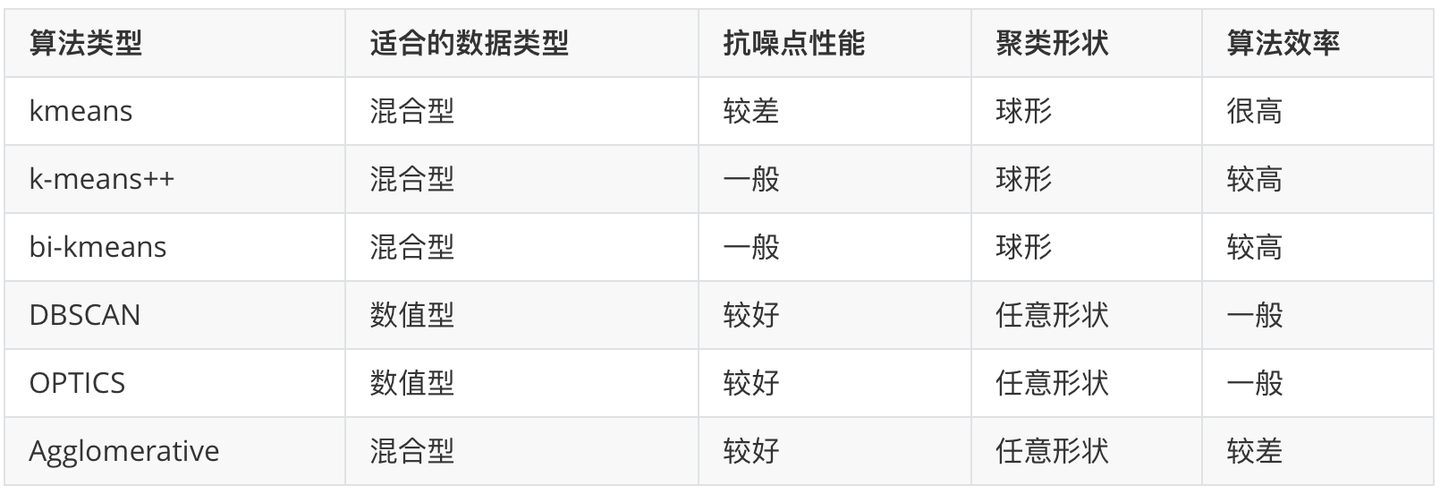
DBSCAN密度聚类
对初值选取敏感,对噪声不敏感。
对密度不均的数据聚合效果不好。
OPTICS密度聚类
对DBSCAN算法的一种有效扩展,主要解决对输入参数敏感的问题。
DBSCAN效果
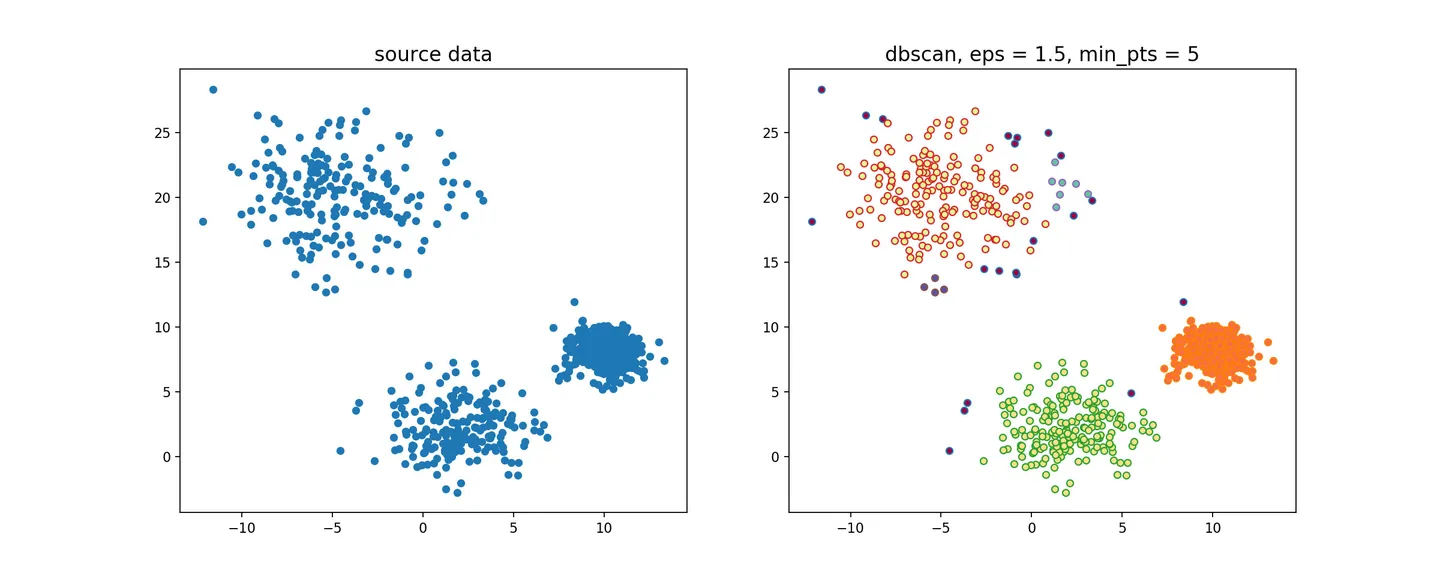
OPTICS效果
Agglomerative层次聚类
又称自底向上的层次聚类。
Divisive层次聚类
又称自顶向下的层次聚类。
图算法
频繁子图挖掘算法
gSpan算法、DFS 编码。
HITS算法
Hub页面(枢纽页面)、Authority页面(权威页面)。
计算效率较低,主题漂移问题,结构不稳定。
PageRank算法
马尔可夫链、计算权重。
寻找最优解
遗传算法(GA)
基因编码。
蚁群算法(ACO)
不容易陷入局部最优。
收敛速度慢。
维特比算法(viterbi)
动态规划。
模拟退火算法
搜索时间越长,获得的最优解更可靠。
评价指标
评价回归
SSE(残差平方和、和方差)
数据和原始数据对应点的误差的平方和
MSE(均方差、方差)
预测值与真实值之间差异的平方和的平均值,越小越好。
RMSE(均方根、标准差)
MSE的平方根,越小越好。
MAE(平均绝对误差)
预测值与真实值之间差异的绝对值的平均值,越小越好。
MPAE(平均绝对百分比误差)
可以比较两个不同尺度的数据之间的差异,越小越好。
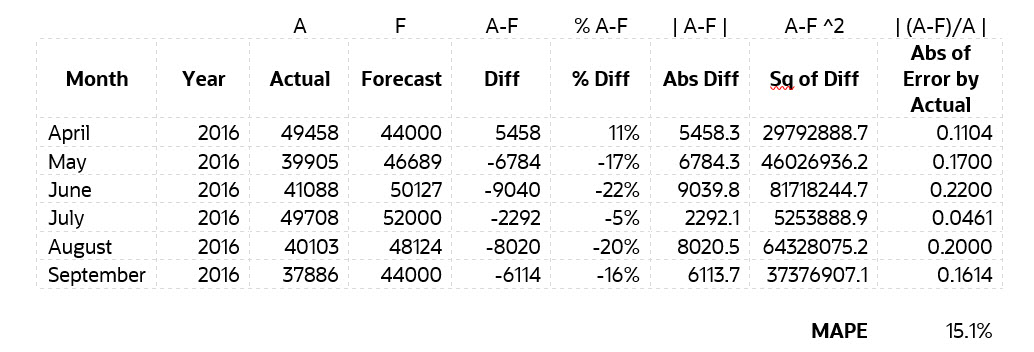
sMAPE 对称平均绝对百分比误差
改进MAPE。
R-squared(确定系数)
通过 SSR(回归平方和)、SST(总偏差平方和)计算得,取值范围为[0 1],越接近1越好。
Adjusted R-squared(调整R方)
单变量线性回归,则使用R-squared评估,多变量,则使用adjusted R-squared。
Huber Loss(霍尔伯损失)
对MSE和MAE的一种折中,它在预测值与真实值相差较大时使用MAE,而在预测值与真实值相差较小时使用MSE。
评价聚类

轮廓系数
轮廓系数S的取值范围为[-1, 1],越大越好。
Calinski-Harabasz指数(方差比准则)
取值范围在(0,+∞)之间,越大越好。
Davies-Bouldin Index(DB指数)
取值范围在[0,+∞)之间,越小越好。
Rand Index(兰德指数)
范围从0到1,1的值表示两个聚类完全相同,接近0的值表示两个聚类有很大的不同。
Adjusted Rand Score(调整兰德指数)
取值范围为[-1, 1],其中1表示聚类结果与真实标签完全一致,0表示聚类结果与真实标签随机一致,-1表示聚类结果与真实标签完全不一致。
Normalized Mutual Information Score(标准化互信息分数)
对互信息的标准化,取值范围为0(没有互信息)到1(完全相关)。
Adjusted Mutual Information Score(调整互信息分数)
调整互信息分数更加稳健,不受标签排序的影响。
Homogeneity and Completeness Score(同质性和完整性)
越大越好。
V-Measure
取值范围为[0, 1],越大越好。
V-Measure对于聚类结果的不确定性更加敏感。
Fowlkes-Mallows Score
基于数据的真实标签和聚类结果的交集、联合集以及簇内和簇间点对数的比值来计算。
邓恩(dunn)指标
取值范围为[0, ∞),越大代表类间距越大、同时类内间距越小。
评价分类
混淆矩阵
各种评价指标的基础。
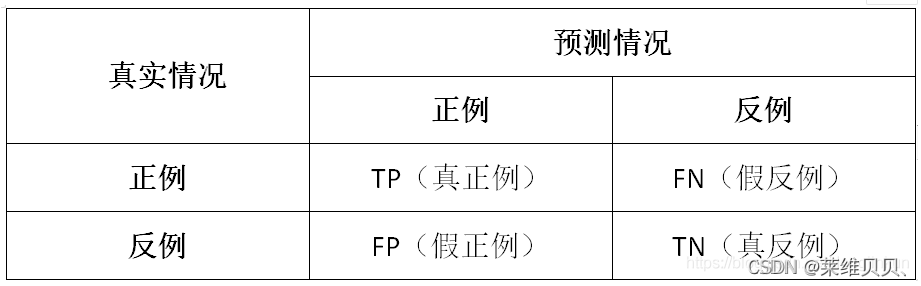
- 真正例(True Positive,TP):一个正例被正确预测为正例。
- 真反例(True Negative,TN):一个反例被正确预测为反例。
- 假正例(False Positive,FP):一个反例被错误预测为正例。
- 假反例(False Negative,FN):一个正例被错误预测为反例。
准确率(Accuracy)
有样本中预测正确的样本占比。
精确率(Precision)
在所有被预测为正的样本中实际为正的样本的概率。
召回率(Recall)
在实际为正的样本中被预测为正样本的概率。
F1-Score
F-Measure是P和R的加权调和平均。
ROC曲线
将真阳性率(True Positive Rate,TPR)和假阳性率(False Positive Rate,FPR)作为横纵坐标来描绘分类器在不同阈值下的性能。
AUC值
AUC是ROC曲线下的面积。
完美的分类器的AUC值为1,而随机分类器的AUC值为0.5。
Hinge Loss(铰链损失)
一种常用于支持向量机(SVM)的损失函数。
Log Loss(对数损失)
常用的分类问题的损失函数。计算的是模型预测概率与真实标签的对数似然。
Softmax交叉熵损失
使用softmax函数将模型预测值转换为概率分布,然后计算该概率分布与真实标签分布之间的差异。
kappa系数
取值为-1到1之间,通常大于0。
